Euklid bis Leibniz

Unsere sozialen Beziehungen werden zunehmend durch Algorythmen ersetzt. Dieser Beitrag zeigt die kulturelle Basis in der Antike und den Wandel im 17. Jahrhundert.

Einen Schachcomputer machen Sie nicht nervös, Sie sind ihm egal. Er kennt nur 0 und 1. Das gilt für unsere ganze moderne Welt. Doch das war nicht immer so. Schauen wir zurück in die Zeit, als menschliche Beziehungen noch Grundlage unseres Handelns waren – und an den Punkt, als unsere heutige Welt geboren wurde.

Wenn Gerechtigkeit relativ ist

Ein Gedankenspiel: „Die Personen A und B spielen ein faires Spiel mehrere Male: Wer als erster 6 Siege errungen hat, soll die eingesetzte Summe erhalten. Nun brechen sie ab bei der Situation, wo A 5 Siege und B 3 Siege aufzuweisen hat. Wie soll die Summe aufgeteilt werden?“

Fühlen Sie sich an Ihre Schulzeit erinnert? Wahrscheinlichkeits-Rechnung? Genau. Wenn Sie nicht gerade Stochastik-Experte sind, werden Sie „aus dem Bauch heraus“ vermutlich sagen: Die beiden Spieler sollen die Summe proportional aufteilen, also im Verhältnis 5:3. Damit befinden Sie sich in guter Gesellschaft, denn genau so antwortete der Autor dieses Problems. Es war kein geringerer als Luca Pacioli (1445–1517), der italienische Mathematiker und Renaissancegelehrte, der als Erfinder der doppelten Buchführung in die Geschichte eingegangen ist.

Porträt Luca Paciolis, gemalt von Jacopo de Barbari, 1495. Mönch und Mathematiker: Fra Luca Pacioli in schwarzgrauer Kutte erläutert einem jungen Adligen geometrische Lehrsätze.

Porträt Luca Paciolis, gemalt von Jacopo de Barbari, 1495. Mönch und Mathematiker: Fra Luca Pacioli in schwarzgrauer Kutte erläutert einem jungen Adligen geometrische Lehrsätze.

Dieser Ruf greift etwas hoch, denn er hat die Idee einer lückenlosen Aufzeichnung aller Geschäftsvorgänge nicht erfunden, aber als erster in einem Buch genau beschrieben. In demselben Buch, in dem er auch dieses Spielproblem diskutierte: „Summa de Arithmetica, Geometria, Proportioni et Proportionalità“, gedruckt in Venedig 1494. (Ich warne Sie schon jetzt, Paciolis Antwort erachten wir heute als falsch! Sie erfahren gleich, warum.)

Titelseite der *Summa de arithmetica, geometria, proportioni, et proportionalita* by Luca Pacioli, 1523 edition. Stockholms Universitetsbibliotek from Stockholm, Sweden, CC BY 2.0

Titelseite der *Summa de arithmetica, geometria, proportioni, et proportionalita* by Luca Pacioli, 1523 edition. Stockholms Universitetsbibliotek from Stockholm, Sweden, CC BY 2.0

Das „analoge“ Denken: Der Mensch als Maß der Dinge

Bei Paciolis „Summa“ handelte es sich wohl um das erste gedruckte Buch eines Mathematikers überhaupt. Darüber hinaus beruht die Bedeutung des Werks nicht etwa auf einzelnen genialen Ideen Paciolis, sondern vielmehr auf seinem fleißigen Zusammentragen von mathematischen Gesetzmäßigkeiten und Erkenntnissen. Es formte ein überaus nützliches und beliebtes Kompendium des gesamten mathematischen Wissens der Zeit.

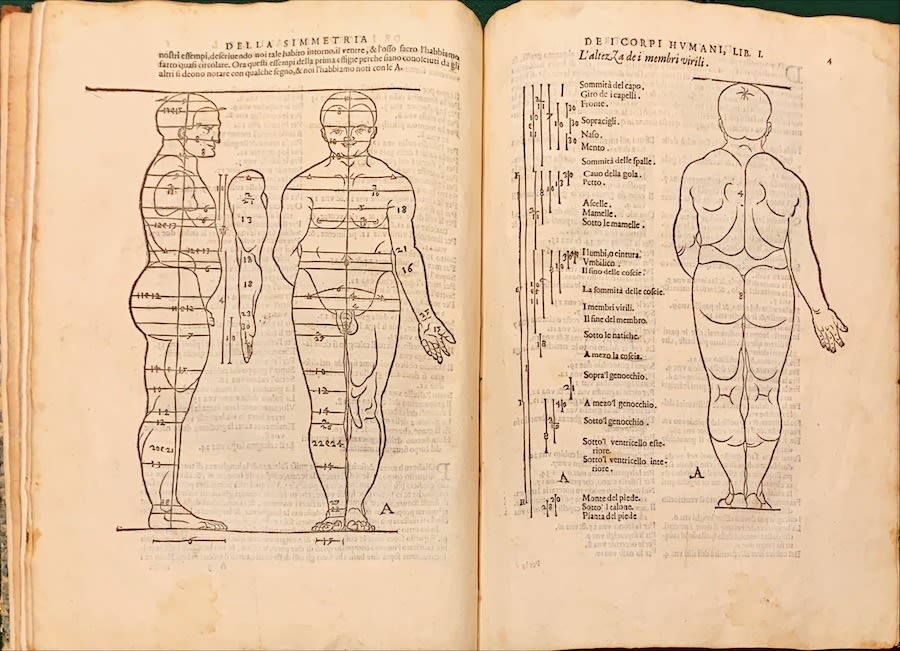
Albrecht Dürer, Della Simmetria, 1594. Ein wichtiges Werk über die menschlichen Proportionen und den Goldenen Schnitt. Dürer (1471-1528) korrespondierte intensiv mit Leonardo da Vinci.

Albrecht Dürer, Della Simmetria, 1594. Ein wichtiges Werk über die menschlichen Proportionen und den Goldenen Schnitt. Dürer (1471-1528) korrespondierte intensiv mit Leonardo da Vinci.

Paciolis Wissen regte auch einen seiner Schüler besonders an: Leonardo da Vinci. Der hochbegabte Jüngling gab seinerseits den Anstoß für eine Abhandlung seines Lehrers über den Goldenen Schnitt, ein zentrales Instrument der Gestaltung für die Renaissancekünstler. Da Vinci illustrierte die „Summa“ ebenso wie er wohl auch zu einem anderen Buch seines Lehrers Zeichnungen beitrug: „De ludo scacchorum“, also „Über das Schachspiel“. Sie erkennen hier die enge Verzahnung von Kunst und Wissenschaft in dieser Epoche.

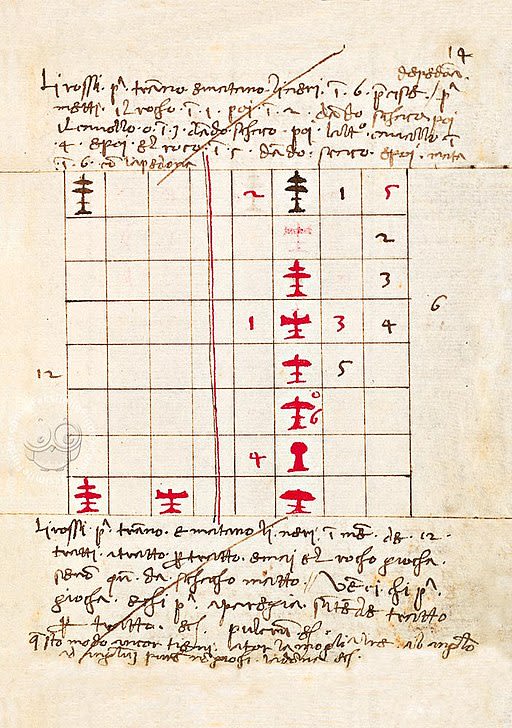
De Ludo Schacorum, Public domain, via Wikimedia Commons

De Ludo Schacorum, Public domain, via Wikimedia Commons

Dieses Schachbuch könnte einem Krimi entsprungen sein. Geschrieben um 1500 genoss es einen exzellenten Ruf und wurde oft zitiert – doch seit Menschengedenken galt es als verschollen. Erst 2006 stieß der Buchhistoriker Duilio Contin auf das bislang einzige bekannte Exemplar in einer Privatbibliothek im norditalienischen Gorizia. Diese Abhandlung wirft ein Schlaglicht auf die Entwicklung des königlichen Spiels, denn zu Paciolis Zeit nahmen die Spielregeln erst ihre bis heute gültige Form an. Anhand der dargestellten Schachprobleme und der Erläuterungen sehen wir, wie alte und neue Regeln nebeneinander bestanden, bevor man die alte Spielweise aufgab.

Doch während im Schach eine neue Zeit angebrochen war, blieb Pacioli in der Mathematik den bisherigen Regeln verhaftet, Regeln der antiken Philosophen, die sich nicht einmal bewusst gewesen waren, dass das eingangs zitierte Problem in das Gebiet der Wahrscheinlichkeitsrechnung fiel. Paciolis Antwort war daher falsch.

In der damaligen Vorstellungswelt (wir nennen sie bisweilen „analog“), waren Tausch- oder Bezahlaktionen niemals Vorgänge unter Laborbedingungen.

Man berücksichtigte stets die beteiligten Menschen und ihre Beziehung.

Als Pacioli seine „Summa“ der mächtigen Markgräfin von Mantua und Mäzenin Isabella d’Este widmete, so sicherte er, der einfache Professor, ihr damit einen Schimmer Ewigkeit und Ruhm. Sie wird sich ihrerseits mit einem Geldgeschenk oder einer anderen Ehrung erkenntlich gezeigt haben. Bei solch einem Gabentausch konnte man in keiner Tabelle einen festen, allgemeingültigen Umrechnungskurs nachschlagen. Es war ein ständiges Austarieren und die Menschen hatten ein Gefühl dafür entwickelt, wem gegenüber was als angemessen galt.

So war es schon in der Antike gewesen, der Zeit, die noch immer die Grundlagen für das Denken in der frühen Neuzeit bildete.

Als Mathematiker stand Pacioli in der Tradition Euklids. Dessen „Elemente“ dienten noch bis ins 19. Jahrhundert als Lehrwerk im Mathematikunterricht. Für lange Zeit galt es als das meistverbreitete Buch gleich nach der Bibel!

Doch wie Pacioli hatte auch Euklid wenig neu entdeckt oder erfunden, sondern vor allem Wissen zusammengetragen. Er betrieb Grundlagenforschung, wie wir aus einer Anekdote erfahren. Einer seiner Schüler soll ihn gefragt haben, was er denn davon habe, all diese Dinge zu lernen. Lakonisch soll Euklid einem Sklaven befohlen haben, dem Schüler ein paar Münzen zu geben. Offenbar habe er es nötig, Geld zu verdienen …

Euklids "Elemente" in 15 Büchern, Basel 1537.

Euklids "Elemente" in 15 Büchern, Basel 1537.

zum Buch

"Punctus est, cuius pars not est."
Der erste Satz in Euklids Elemente gibt den Tonfall an.

Übersetzungen ins Arabische verdanken wir, dass die Schriften des antiken Mathematikers erhalten blieben. Die Gelehrten des Orients verstanden den Wert von Euklids Schriften, in denen die strenge Mathematik in kaum zu überbietender Trockenheit kondensiert war. Sofort geht es zur Sache: "Ein Punkt ist, was keine Teile hat" lautet der erste Satz, und in dem Stil geht es weiter: Punkte, Geraden, Kreise bebildern in dichter Folge kurze Aussagesätze, die ständig Vorangegangenes voraussetzen. Wer sollte das verstehen?

Euclidis Megarensis Mathematici Clarissimi Elementorum geometricorum

Die Antwort darauf ist eine andere Frage: Wie soll man das verstehen? Der irische Mathematiker Oliver Byrne versuchte sich mit einem Ansatz, der in unserer Zeit des visuellen Überflusses überaus modern anmutet. Byrne schuf das vielleicht schönste Mathematikbuch aller Zeiten. Im Jahr 1847 veröffentlicht er in einer Auflage von 1.000 Exemplaren eine Ausgabe der ersten sechs Bücher von Euklids „Elemente“. Damals galt sein Buch weniger als ernsthafte Arbeit denn als verschrobene Kuriosität. Byrne illustrierte nämlich die hochkomplexen mathematischen Formeln und Gleichungen des antiken Mathematikers mit vielen farbigen Grafiken, die in ihrem geometrischen Auftreten einem Bauhaus-Katalog entsprungen sein könnten. Es handelte sich dabei übrigens um eines der ersten mehrfarbig gedruckten und nicht von Hand kolorierten Bücher.

The Elements of Euclid, The first six Books, by Byrne Oliver. Faksimile des Originals von 1847

Geometrische Flächen, satte Primärfarben, schwarze Linien: das erinnert an Mondrian. Doch bereits ein knappes Jahrhundert zuvor war es der Mathematiker Oliver Byrne, der dasselbe Farbschema auf seine 1847er-Ausgabe von Euklids arithmetischer und geometrischer Abhandlung Die Elemente anwandte. Byrnes Idee war es, Farbe zur Erleichterung des Verständnisses einzusetzen.

Doch zurück zu Euklid. Bei all seiner mathematischen Brillanz stand doch auch er wiederum in der Tradition des Aristoteles. Wenn wir zurückkehren zu unserer Frage, inwieweit der Mensch sich als Größe immer wieder in das „analoge“ Denken schlich, dann erinnern wir uns an Aristoteles’ Aussage, ein gerechter Tausch berücksichtige stets auch die Beziehung der Tauschenden. Diese moralische Ebene galt auch für Aktionen wie das eingangs beschriebene mathematische Wahrscheinlichkeitsproblem. Oder für die Frage, was Isabella d’Este dem Mathematiker Pacioli für seine Widmung ihrerseits zu schenken hätte. Für Pacioli war klar, 5 Siege gegen 3, also bekommt einer 5 Teile der Siegessumme, der andere 3.

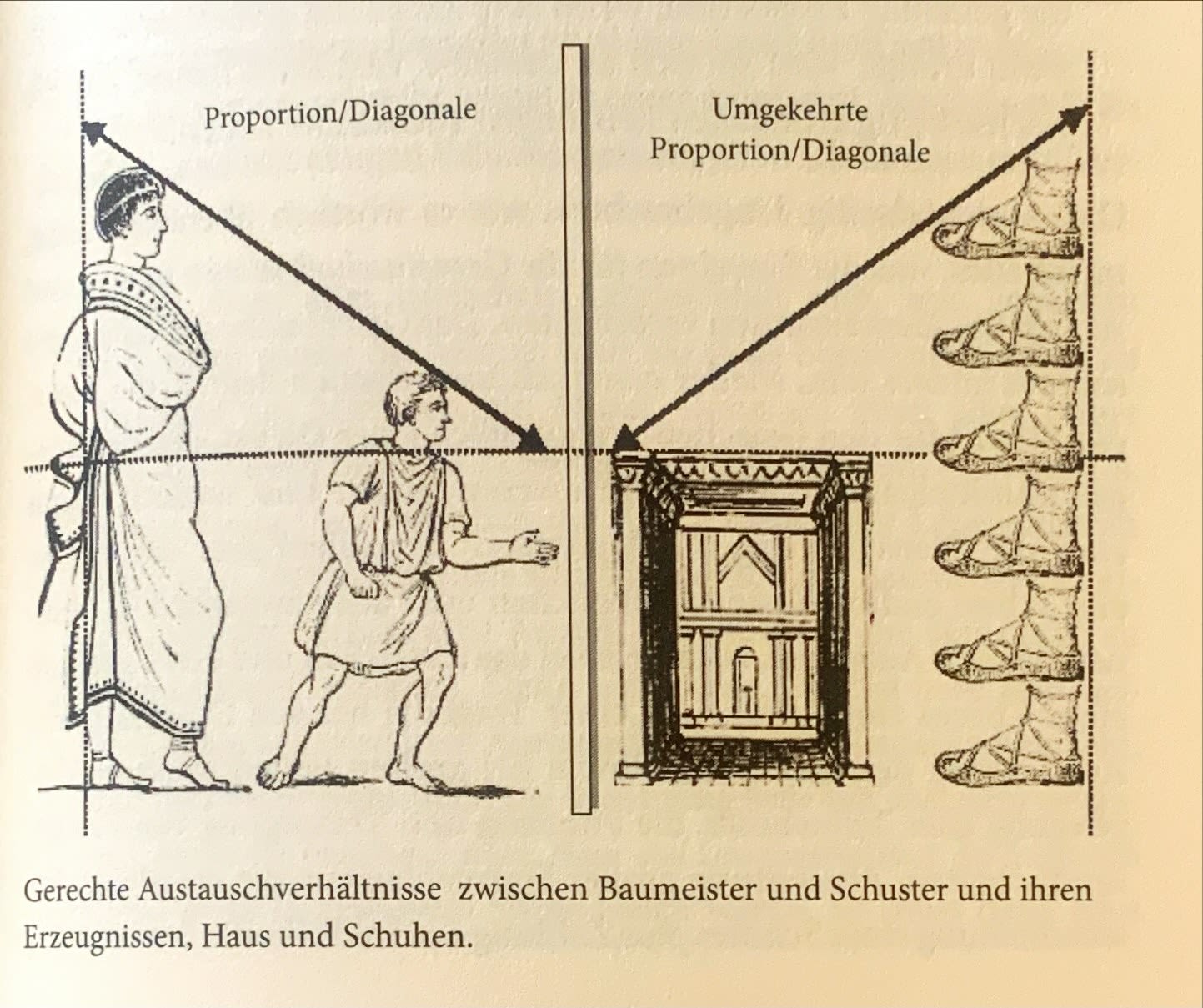
Eske Bockelmann, Das Geld, Was es ist, das uns beherrscht, Berlin 2020, Seite 127: Es sind nach Aristoteles vier Grössen zu berücksichtigen beim gerechten Ausgleich: nicht nur die zwei getauschten Güter, sondern auch die beiden Tauschenden selbst. Wenn zum Beispiel ein Baumeister vom Schuster dessen Werkstücke bekommt und ihm dafür das seinige als Gegenleistung überlässt, so gelte: wie sich der Baumeister zum Schuster verhält, so muss sich die Leistung des Schusters zu der des Baumeisters verhalten.

Eske Bockelmann, Das Geld, Was es ist, das uns beherrscht, Berlin 2020, Seite 127: Es sind nach Aristoteles vier Grössen zu berücksichtigen beim gerechten Ausgleich: nicht nur die zwei getauschten Güter, sondern auch die beiden Tauschenden selbst. Wenn zum Beispiel ein Baumeister vom Schuster dessen Werkstücke bekommt und ihm dafür das seinige als Gegenleistung überlässt, so gelte: wie sich der Baumeister zum Schuster verhält, so muss sich die Leistung des Schusters zu der des Baumeisters verhalten.

Erst der Philosoph Blaise Pascal beantwortete das Problem im Jahr 1654 im Sinne der Wahrscheinlichkeitsrechnung richtig. Die Summe, so Pascal, müsse im Verhältnis 7:1 geteilt werden. Man müsse berücksichtigen, wie wahrscheinlich ein Sieg der Spieler war, wenn sie weitergespielt hätten. Es kommt jetzt nicht mehr darauf an, dass die beiden Spieler ihrem Gefühl nach angemessen entschädigt wurden. Bei Pascal herrschte die pure Mathematik, das Durchrechnen von Möglichkeiten, Wahrscheinlichkeiten, Fortsetzungen in der Zukunft. Willkommen in der modernen Welt, im „digitalen“ Denken. Willkommen im Heute!

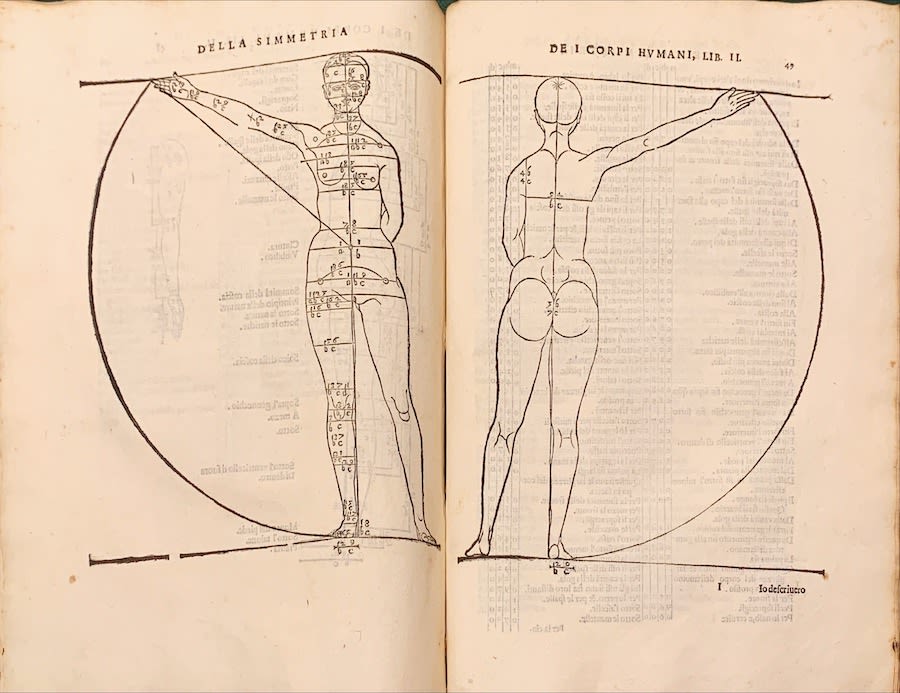
Albrecht Dürer, Della Symmetria, 1594. Dürer stellte die menschlichen Proportionen dar.

Albrecht Dürer, Della Symmetria, 1594. Dürer stellte die menschlichen Proportionen dar.

Die Geburt des „digitalen“ Denkens: Gott und das Nichts, 1 und 0

Was war passiert zwischen Pacioli und Pascal? Nichts Geringeres als eine Revolution. Der Revolutionär? Ein reaktionärer, gottesgläubiger Protestant, der Gelehrte Gottfried Wilhelm Leibniz (1646–1716)!

Was Descartes am Anfang des 17. Jahrhunderts ahnte, nämlich die Teilung der Welt in Subjekt und Objekt, findet in Leibniz am Ende des Jahrhunderts eine Art Krönung. Ironischerweise war es auch der Glaube des letzten Universalgelehrten, der Leibniz die Welt binär sehen ließ. Leibniz entwickelte die sogenannte „Dyadik“, ein Zahlensystem, in dem alle Zahlen nur mit 0 oder 1 dargestellt wurden. Auf dieser auf den ersten Blick vollkommen verrückten Idee beruht jeder moderne Computer!

Leibniz entwickelte eine Rechenmaschine, die er auch noch viermal verbesserte. Vermutlich funktionierte keines der Geräte besonders gut, weil die feinmechanischen Herausforderungen die zeitgenössischen Möglichkeiten überstiegen; erst 1990 gelang ein funktionstüchtiger Nachbau. Doch die Erfindung war bezeichnend für den Schritt in die Moderne, den ihr Erfinder tat: „Es ist unwürdig, die Zeit von hervorragenden Leuten mit knechtischen Rechenarbeiten zu verschwenden ...“

Leibniz' Rechenmaschine. Bild und Text LeibnizCentral.de: "Als der Universalgelehrte Gottfried Wilhelm Leibniz 1673 das erste Modell einer Rechenmaschine vorstellte, die alle vier Grundrechenarten beherrscht, war das ein Meilenstein der technologischen Entwicklung. Über vier Jahrzehnte hinweg entwickelte Leibniz die Maschine."

Leibniz' Rechenmaschine. Bild und Text LeibnizCentral.de: "Als der Universalgelehrte Gottfried Wilhelm Leibniz 1673 das erste Modell einer Rechenmaschine vorstellte, die alle vier Grundrechenarten beherrscht, war das ein Meilenstein der technologischen Entwicklung. Über vier Jahrzehnte hinweg entwickelte Leibniz die Maschine."

Leibniz überzog diese sehr moderne Weltsicht mit einem binären Netz von Einen und Nullen. Denn nicht nur die Mathematik bestand für ihn aus 1 und 0, die ganze Welt ließ sich so beschreiben. Immerhin glaubte auch Leibniz im Sinne der antiken Pythagoräer, dass sich die ganze erfahrbare Welt durch eine mathematische Brille betrachten lasse: unsere Sprache, ja die Denkprozesse in unserem Kopf, alles ist irgendwie in Zahlen enthalten und beruht auf Zahlen.

Der gläubige Christ Leibniz folgte dabei der Prämisse: „Ohne Gott ist nichts.“ Dies führte ihn zu der Gleichung: Gott ist 1, das Nichts ist 0. Dies war keine moralische Wertung der Zahlen oder der Welt, sondern eine pure Beschreibung – die uns alles andere als modern anmuten mag. Sie findet eine Parallele in der fernöstlichen Vorstellung von Yin und Yang, den sich entgegenstehenenden Kräften, die sich aber nicht im Sinne eines Gut und Böse bekämpfen, sondern ergänzen und gegenseitig bedingen.

Ist unsere binäre Welt die beste mögliche?

Leibniz versuchte, die Welt zu verstehen und strebte nach einer universellen Harmonie. Seine Ideen halfen mit, die bisherige Weltsicht endgültig über den Haufen zu werfen. Unser Blick geht seither immer zur Zukunft hin, durch zwei Brillengläser, auf denen 1 und 0 steht.

Und Veränderung ist der moderne Aspekt dieses Weltbildes. Als Leibniz den bis heute meist missverstandenen Ausspruch tat, unsere Welt sei „die beste aller möglichen Welten“, rief er nicht dazu auf, sich zufrieden in seinem Lehnstuhl auszuruhen. Im Gegenteil! Leibniz verstand unsere Welt als veränderbar, dynamisch, voller Potenzial. Wir können aus dem, was ist, das formen, was sein soll; das Beste, was wir uns nur vorstellen können.

Das binäre Zahlensystem hat zu den Algorithmen geführt - Google, Facebook, ja sogar Ihr smarter Kühlschrank funktioniert mit Algorithmen. Menschliche Beziehungen haben als Operatoren zumindest in Wirtschaft und Technik keinen Platz mehr.

Ein Raum voller mathematischen Formeln.

Ein Raum voller mathematischen Formeln.

Diese Revolution im Denken trat ein, als das moderne Kreditgeld aufkam und die Marktwirtschaft sich als das vorherrschende Wirtschaftssystem etablierte. Ein Zufall?

Wohl nicht. Die Subjekt-Objekt Spaltung, die Descartes als erster ahnte, findet ihre Konsequenz in den 1 Und 0 von Leibniz. Ihr Ursprung aber liegt, nach Eske Bockelmann, im sog. Denkreflex, der sich im 16. Jahrhundert herausbildete. Und dieser hat sehr viel mit unserem modernen Geld zu tun.