Leonardo Fibonaccy da Pisa (english)

Fibonacci, the principle of Growth

Who was Leonardo of Pisa and when was his book published? And what does he have to do with Fibonacci?

Leonardo of Pisa, better known as Leonardo Fibonacci, lived from about 1170 to after 1240 and is considered the first important mathematician in Europe. On journeys to Africa, Byzantium and Syria, he became acquainted with Arabic mathematics, which was largely unknown in the Christian West. He combined this knowledge with his own reflections in his work "Liber abaci", which appeared in 1202. The book remained unsurpassed in the history of Western mathematics for a long time and contributed, among other things, to Europe's adoption of the Arabic number system.

In the Liber abaci there is a thought experiment which Fibonacci himself probably regarded as a mere curiosity and did not pursue, but which was later to become famous as the "Fibonacci sequence".

Fibonacci asked himself how many pairs of rabbits descended from a single pair in one year. He assumed that no rabbits die within this year and that each pair of rabbits produces exactly one pair of both sexes per month, which in turn is fertile from the second month after birth.

Where does the Fibonacci series of numbers come from? In his book "Liber abaci" he writes: "Because the above pair already gives birth in the first month, you can double it so that after one month there are two pairs."

At the end of the first month, where Fibonacci begins his count, two pairs of rabbits exist.
At the end of the second month, the original pair has given birth to another pair, the other pair became procreative. Now there are 3 pairs.
Of these 3 pairs, in the third month, two are now fertile and one is not, so at the end of the next month, two more pairs of rabbits are added, there are now a total of 5 pairs.
Of these 5 pairs, 3 again become pregnant, that in the fourth month there are 8 pairs.
Um die Zahl der Kaninchenpaare zu ermitteln, beobachtete Fibonacci, muss man also nichts anderes tun, als jeweils die Summe der Kaninchenpaare der beiden vorangegangenen Monate zusammenzuzählen.

At the beginning there is one pair of rabbits. After one month there are 2 pairs of rabbits, after two months there are 1 plus 2, i.e. 3, after three months 2 plus 3, i.e. 5, after four months 3 plus 5, i.e. 8, etc. - until after eleven months there are 233 pairs of rabbits from the first pair.

Although Fibonacci's thought experiment is of course based on unrealistic assumptions, it describes essential features of growth processes. While for Fibonacci his task was thus solved, it was later discovered that the Fibonacci sequence can be found in nature and art - be it in the leaf position of plants, in the spiral shape of shells, in the cloud structure of a low-pressure area or in paintings, architectural structures or music.

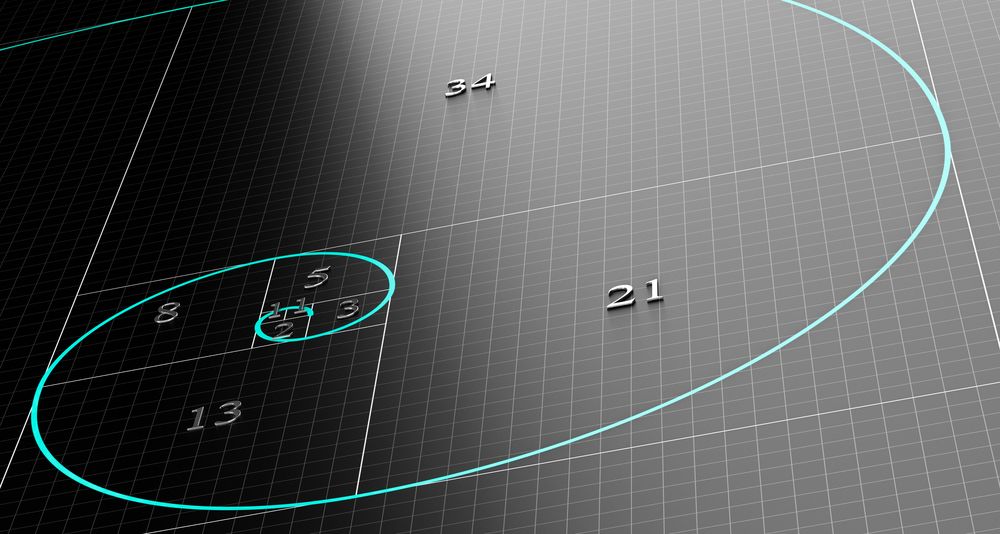
One can also approach the Fibonacci numbers geometrically. Let's start from a square with side length 1. Next to it we construct a second square of the same size. We connect another square to it, which has the side length 2. Then we construct a square with side length 3, one with side length 5, one with side length 8. You can easily recognize the numbers of the Fibonacci sequence.

Now we draw a quarter circle in each square. The spiral that results is called a Fibonacci spiral. It can be seen very clearly in the Nautilus shell.

The golden section and its relatives

The first precise description of the golden section - he called it "division according to the outer and middle ratio" - was provided by the Greek mathematician Euclid as early as 300 B.C.: A line is divided into two parts in such a way that the smaller part relates to the larger part in exactly the same way as the larger part relates to the whole. Later, in the 15th century, the Italian mathematician and Franciscan monk Luca Pacioli studied Euclid's work and dedicated an entire volume to this division of a line, which he called "proportio divina," or "divine division".

Luca Pacioli: «proportio divina»

Luca Pacioli: «proportio divina»

Around 1600, Johannes Kepler - known for Kepler's laws of planetary motion - discovered the relationship between the Fibonacci numbers and the golden ratio. He noticed that the ratio between a number of the Fibonacci sequence and the preceding one approaches more and more the irrational number Φ ((Phi)), the longer one continues the sequence. And Φ denotes nothing else than the golden ratio.

The golden ratio defines a proportion that has always been perceived by the human perceptual system as particularly beautiful and harmonious. We can find its application for many epochs in almost all cultures around the world, especially in architecture and art.

A rectangle whose aspect ratio corresponds to the golden ratio is called a golden rectangle. Likewise, isosceles triangles with two sides in this ratio are called Golden Triangles.

The Pentagram

The pentagram is a regular, five-pointed star, which arises from the diagonals of a regular pentagon and was already considered a magical sign in ancient times.

The pentagram can also be thought of as a composition of five golden triangles. If one connects the five points of intersection in the inside, another pentagram is formed there. Even if one draws in its inner pentagon again a pentagram and so on, all triangles which are contained in this drawing are golden triangles.

If you cut an apple crosswise, you will find a natural image of the pentagram in the core. Like all rose plants, the apple is associated with the feminine, the life-giving principle. So it is not surprising that the pentagram is the symbol of Venus, both the planet and the goddess. Since you can draw the symbol in one go and come back to the beginning at the end, it was also considered a sign of the cycle of life. In the Middle Ages, the pentagram, the "druid's foot", was used as a sign to ward off demons.

And even today it is omnipresent: the stars of numerous flags, for example those of the USA or the EU, are pentagrams. The symbol of Islam or the Soviet star are also pentagrams.

The Fibonacci numbers in nature

The frequent occurrence of the golden section and Fibonacci numbers in nature is surprising. Most strikingly, these structural principles are found in the phyllotaxy of plants, i.e. the arrangement of leaves and seed pods. In many more highly developed plant species, the angle between leaves that follow one another in a spiral pattern averages around 137.5 degrees - the golden angle. This leaf arrangement is also known as Fibonacci phyllotaxy.

Since the golden angle is based on an irrational number, one leaf will never be exactly above the other. The sunlight falling from above can therefore be used optimally and incoming rain is passed on by the leaves to the roots in maximum quantity.

In the sunflower, phyllotaxy appears in a particularly aesthetic form in the so-called parastiches, the spirally arranged seed capsules on the flower base.

The clearly recognizable Fibonacci spirals are not formed from seeds that follow one another in terms of growth, but rather result from the fact that successive seeds are arranged offset by the golden angle; the deviation from the mathematical golden angle is less than 0.01 percent.

If you look at the number of arcs turning left and the number of arcs turning right, you will hardly be surprised: These are also consecutive Fibonacci numbers. In the outer part of sunflowers, one usually counts 34 and 55 spirals, in larger specimens 55 and 89, or even 89 and 144. Whether the larger number are right- or left-turning arcs, however, is left to chance.

This animation shows a constructed inflorescence with 200 seeds. Starting from the germination center, the seeds migrate outward as they grow until the entire flower head is filled.

Successive seeds emerge exactly offset from each other by the golden angle, as the seeds are most densely packed in this way. This can be illustrated by changing the angle between two successive seeds in terms of growth.

As we can see, 13 and 21 Fibonacci spirals are formed here. Translated with www.DeepL.com/Translator (free version)

The Golden Section in Architecture and Art

Since time immemorial, we find the golden proportion wherever people wanted to express beauty and where they tried to approach the divine ideal. These are in general the arts, and in architecture in particular the sacred sites.

Already in the pyramids of Giza the proportions of the number Phi are shown in astonishing accuracy. For example, in the Pyramid of Khufu, the ratio of the length of the side of the pyramid to half of the base of the pyramid is 356 : 220 cubits, equal to 1.618, the number Phi.

The golden measurements are also found in the most famous of the great stone monuments, Stonehenge, built about 3500 years ago near Salisbury in England.

The Parthenon of Athens, built in 450 BC under Pericles, is one of the most famous classical buildings. It is also considered to be the most beautiful and most complete work of ancient Greek architecture.

It incorporates the proportions of the golden section in many ways and with astonishing accuracy.

From 1940, the architect and painter Le Corbusier developed a unified tool of measurement, in which metrics are replaced by a scale of harmonic dimensions derived from human proportions and the golden ratio. In his book "The Modulor", in which he published these ideas, and which today is one of the most important works of architectural theory, he writes:

"A human being with raised arm provides in the main points of space displacement - foot, solar plexus, head, fingertip of the raised arm - three intervals that give a series of golden sections named after Fibonacci."

In art, the proportions of the golden section can be seen in the basic structure of numerous famous paintings such as "The Last Supper" by Leonardo da Vinci or Albrecht Dürer's "Self Portrait". An artist of modern times who consciously uses the golden ratio is, for example, the Dutch painter Piet Mondrian.

In the large hall of Zurich's main station, one can also find an example of a contemporary application of the Fibonacci numbers in the visual arts. The installation "Ovus philosophicus" by the Italian artist Mario Merz.

Within music, the golden ratio appears in several forms.

Just observing a piano keyboard is interesting. The interval of an octave from small C to C1 includes 8 white keys and 5 black keys, for a total of 13 keys. The black keys are divided into groups of 2 and 3. All numbers and ratios from the Fibonacci series.

In the works of the musicologist Ernö Lendvai we read that the golden ratio and the Fibonacci numbers can be found as a dominating design principle in the works of the composer Béla Bartok.

This is particularly evident in the Sonata for Two Pianos and Percussion, where not only the formal parts follow the proportions of the Golden Section. Bartok himself, whose favorite flower is said to have been the sunflower, never commented on this, however.

There are similar studies on works by Bach, Mozart, Schubert, Debussy or Satie. Last but not least, the golden ratio can also be found in the construction of musical instruments.

The Fibonacci numbers and Mandelbrot's fractals

The American-French mathematician Benoît Mandelbrot is largely responsible for the emergence of interest in fractal geometry and chaos theory in the 1980s.

Fractals are initially just mathematically defined objects that are not one, two or three dimensional, but something in between. It is not possible to imagine them vividly. Nevertheless, objects exist in nature that come close to such fractals. In them one finds repeating structures, which are similar to each other at rough observation as well as in detail. One speaks therefore also of self-similarity.

A particularly nice example of fractal geometry in nature is the romanesco, a green cauliflower.

However, the popularity of fractals has probably been due less to their scientific significance than to the possibility of creating images of high aesthetic appeal on the computer using simple algorithms. The most famous of them is probably the "apple man" or the Mandelbrot set. In its marginal areas, it shows similar but always new and amazingly beautiful structures at every enlargement.

What do the fractals have to do with the Fibonacci numbers? The different sized apple shapes of the Mandelbrot set arise in different periods of repetition of mathematical algorithms. If one looks now at these apple forms, the following can be determined: Of all the apples between an apple of period 2 and an apple of period 3, the apple of period 5 is the largest. Likewise, of all the apples between the one of period 5 and the one of period 3, the apple of period 8 is the largest. And of all the apples between the one of period 8 and the one of period 5, it is again the apple of period 13. All numbers from the Fibonacci series.