Euclid to Leibniz

How our social relationships are increasingly replaced by algorythms

You don't make a chess computer nervous, it doesn't care about you. It only knows 0 and 1. This is true for our entire modern world. But it was not always so. Let's look back to the time when human relationships were still the basis of our actions - and to the point when our present world was born.

When justice is relative

A thought experiment: "The persons A and B play a fair game several times: Whoever has won 6 victories first shall receive the staked sum. Now they break off at the situation where A has 5 victories and B has 3 victories. How should the sum be divided?"

Do you feel reminded of your school days? Probability calculation? Exactly. Unless you're a stochastics expert, you'll probably say "by instinct": let the two players divide the sum proportionally, i.e., in the ratio 5:3. You're in good company with that, because that's exactly how the author of this problem answered it. It was none other than Luca Pacioli (1445-1517), the Italian mathematician and Renaissance scholar who has gone down in history as the inventor of double-entry bookkeeping.

Portrait of Luca Pacioli, painted by Jacopo de Barbari, 1495

Portrait of Luca Pacioli, painted by Jacopo de Barbari, 1495

This reputation reaches a bit high, because he did not invent the idea of a complete record of all business transactions, but he was the first to describe it precisely in a book. In the same book in which he also discussed this game problem: "Summa de Arithmetica, Geometria, Proportioni et Proportionalità", printed in Venice 1494. (I warn you already now, Pacioli's answer we consider wrong today! You will learn why in a moment).

Title page of Summa de arithmetica, geometria, proportioni, et proportionalita by Luca Pacioli, 1523 edition. Stockholms Universitetsbibliotek from Stockholm, Sweden, CC BY 2.0

Title page of Summa de arithmetica, geometria, proportioni, et proportionalita by Luca Pacioli, 1523 edition. Stockholms Universitetsbibliotek from Stockholm, Sweden, CC BY 2.0

"Analog" thinking: Man as the measure of all things

Pacioli's "Summa" was probably the first book ever printed by a mathematician. Moreover, the importance of the work is not based on Pacioli's individual brilliant ideas, but rather on his diligent compilation of mathematical laws and findings. It formed an extremely useful and popular compendium of the entire mathematical knowledge of the time.

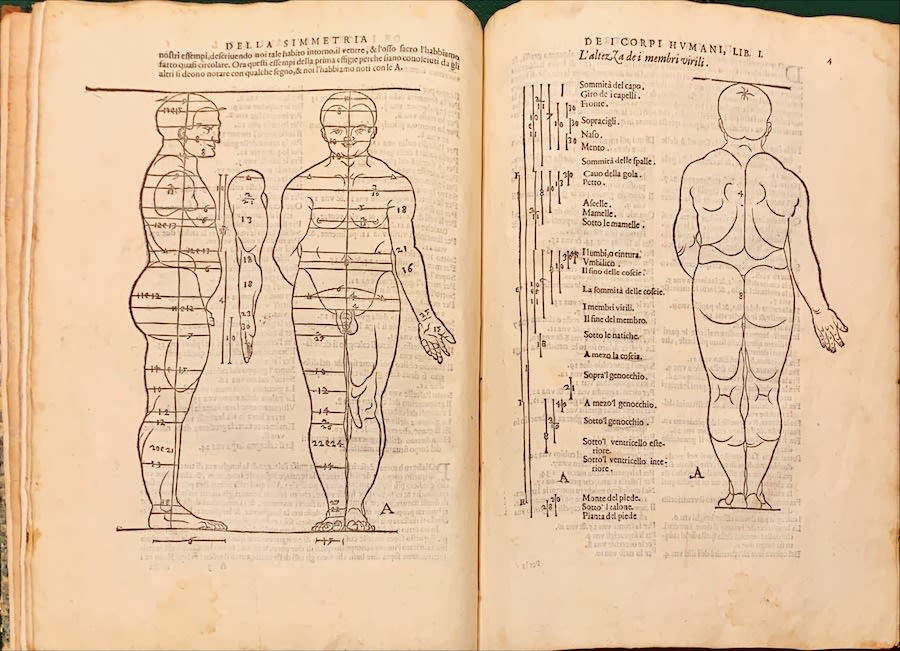
Albrecht Dürer, Della Simmetria, 1594, an important work on human proportions and the golden ratio. Dürer (1471-1528) corresponded intensively with Leonardo da Vinci.

Albrecht Dürer, Della Simmetria, 1594, an important work on human proportions and the golden ratio. Dürer (1471-1528) corresponded intensively with Leonardo da Vinci.

Pacioli's knowledge also particularly stimulated one of his students: Leonardo da Vinci. The highly gifted young man, for his part, provided the impetus for a treatise by his teacher on the golden section, a central instrument of design for Renaissance artists. Da Vinci illustrated the "Summa" just as he probably also contributed drawings to another of his teacher's books: "De ludo scacchorum", i.e. "On Chess". You can see here the close interlocking of art and science in this epoch.

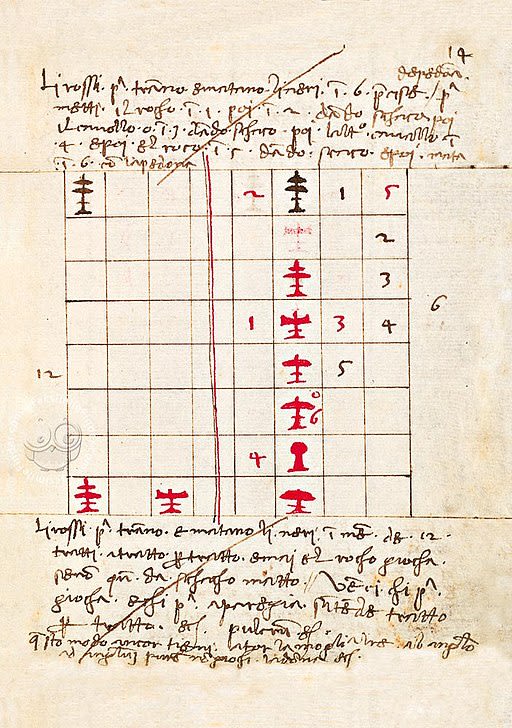
De Ludo Schacorum, Public domain, via Wikimedia Commons

De Ludo Schacorum, Public domain, via Wikimedia Commons

This chess book could have come out of a detective story. Written in the 1500s, it enjoyed an excellent reputation and was often cited - but for as long as anyone can remember, it was considered lost. It was only in 2006 that the book historian Duilio Contin came across the only known copy to date in a private library in Gorizia in northern Italy. This treatise sheds light on the development of the royal game, for it was in Pacioli's time that the rules of the game first took on the form that is still valid today. Through the chess problems presented and the explanations, we see how old and new rules coexisted before the old way of playing was abandoned.

But while a new era had dawned in chess, Pacioli remained attached to the previous rules in mathematics, rules of the ancient philosophers, who had not even been aware that the problem quoted at the beginning fell into the field of probability theory. Pacioli's answer was therefore wrong.

In the imaginary world of the time (we sometimes call it "analog"), exchange or payment actions were never processes under laboratory conditions.

One always considered the people involved and their relationship.

When Pacioli dedicated his "Summa" to the powerful countess of Mantua and patron Isabella d'Este, he, the simple professor, thereby secured for her a glimmer of eternity and fame. She, in turn, will have reciprocated with a gift of money or some other honor. In such an exchange of gifts, one could not look up in any table a fixed, universal rate of conversion. It was a constant balancing act, and people had developed a sense of what was considered appropriate to whom.

This is how it had been in antiquity, the time that still formed the foundations for thinking in the early modern period.

As a mathematician, Pacioli stood in the tradition of Euclid. His "Elements" served as a textbook in mathematics classes until the 19th century. For a long time, it was considered the most widely read book right after the Bible!

However, like Pacioli, Euclid had not discovered or invented much, but rather gathered knowledge. He conducted basic research, as we learn from an anecdote. One of his students is said to have asked him what he got out of learning all these things. Laconically, Euclid is said to have ordered a slave to give the student a few coins. Apparently he needed to earn money ...

Euklids "Elemente" in 15 Büchern, Basel 1537.

Euklids "Elemente" in 15 Büchern, Basel 1537.

"Punctus est, cuius pars not est."
The first sentence in Euclid's Elements sets the tone.

Thanks to translations into Arabic, the writings of the ancient mathematician have been preserved. The scholars of the Orient understood the value of Euclid's writings, in which the strict mathematics was condensed in hardly surpassable dryness. The first sentence is "A point is what has no parts", and it continues in this style: points, straight lines, circles form short statements in dense sequence, which constantly presuppose the preceding. Who should understand this?

Euclidis Megarensis Mathematici Clarissimi Elementorum geometricorum

The answer to this is a different question: How is one to understand this? The Irish mathematician Oliver Byrne tried an approach that seems exceedingly modern in our age of visual abundance. Byrne created perhaps the most beautiful mathematics book of all time. In 1847, he published an edition of 1,000 copies of the first six books of Euclid's Elements. At the time, his book was considered less a serious work than a quirky curiosity. Byrne illustrated the highly complex mathematical formulas and equations of the ancient mathematician with many colorful graphics, which in their geometric appearance could have sprung from a Bauhaus catalog. Incidentally, this was one of the first books printed in multiple colors and not colored by hand.

The Elements of Euclid, The first six Books, by Byrne Oliver. Faksimile des Originals von 1847

Geometric surfaces, rich primary colors, black lines: this is reminiscent of Mondrian. But barely a century earlier, it was the mathematician Oliver Byrne who applied the same color scheme to his 1847 edition of Euclid's arithmetical and geometrical treatise The Elements. Byrne's idea was to use color to facilitate understanding.

A facsimile of Byrne's colorful work is available from Taschenverlag as part of the Bibliotheca Universalis series.

With an afterword by Werner Oechslin, founder of the Werner Oechslin Library in Einsiedeln.

But back to Euclid. For all his mathematical brilliance, he too was in the tradition of Aristotle. If we return to our question to what extent man as a quantity always crept into "analog" thinking, then we remember Aristotle's statement that a just exchange always takes into account the relationship of the exchangers. This moral level also applied to actions like the mathematical probability problem described at the beginning. Or for the question of what Isabella d'Este would have to give the mathematician Pacioli for his dedication on her part. For Pacioli it was clear, 5 victories against 3, so one gets 5 parts of the victory sum, the other 3.

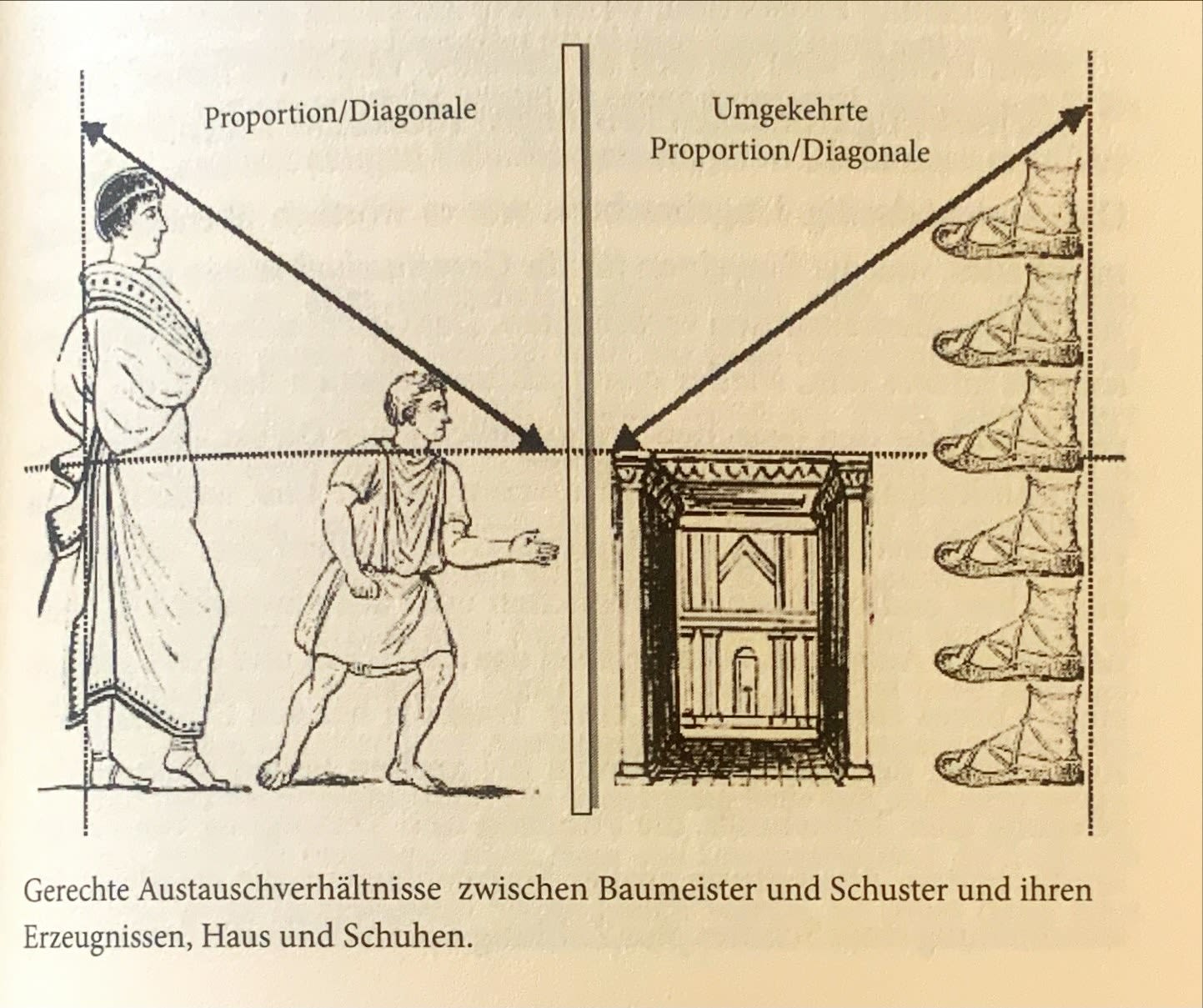
Eske Bockelmann, Das Geld, Was es ist, das uns beherrscht, Berlin 2020, page 127: According to Aristotle, there are four quantities to be taken into account for a fair compensation: not only the two exchanged goods, but also the two exchangers themselves. If, for example, a builder receives from the shoemaker his workpieces and gives him his own in return, then the following applies: as the builder relates to the shoemaker, so must the performance of the shoemaker relate to that of the builder.

Eske Bockelmann, Das Geld, Was es ist, das uns beherrscht, Berlin 2020, page 127: According to Aristotle, there are four quantities to be taken into account for a fair compensation: not only the two exchanged goods, but also the two exchangers themselves. If, for example, a builder receives from the shoemaker his workpieces and gives him his own in return, then the following applies: as the builder relates to the shoemaker, so must the performance of the shoemaker relate to that of the builder.

Only the philosopher Blaise Pascal answered the problem correctly in 1654 in terms of probability theory. According to Pascal, the sum had to be divided in a ratio of 7:1. One had to take into account how likely it was that the players would win if they had continued to play. What matters now is not that the two players felt they had been adequately compensated. With Pascal, pure mathematics prevailed, the calculating of possibilities, probabilities, continuations in the future. Welcome to the modern world, to "digital" thinking. Welcome to today!

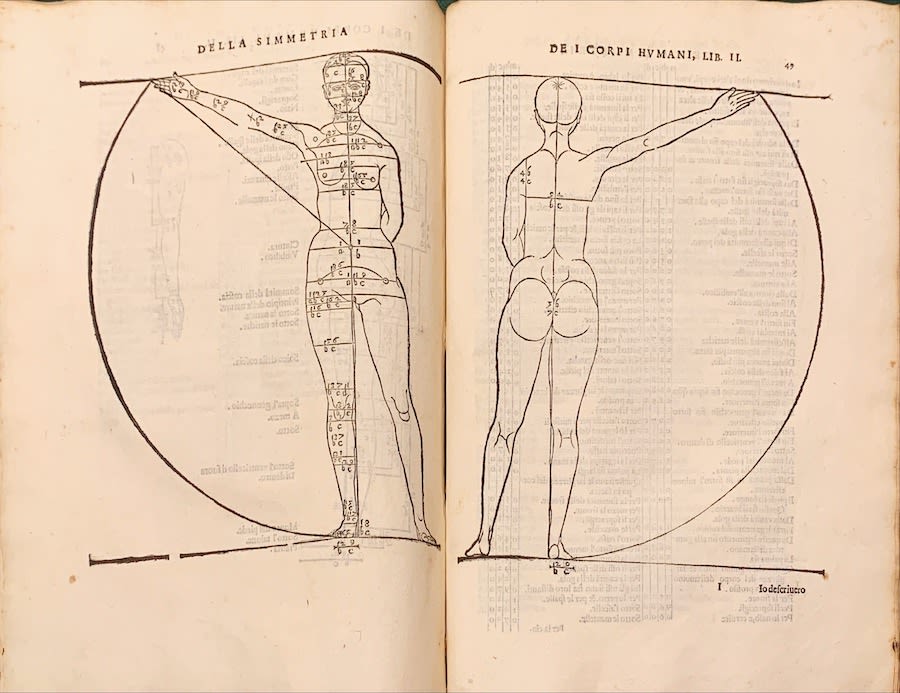
Albrecht Dürer, Della Symmetria, 1594. Dürer depicted human proportions.

Albrecht Dürer, Della Symmetria, 1594. Dürer depicted human proportions.

The Birth of "Digital" Thinking: God and Nothingness, 1 and 0

What had happened between Pacioli and Pascal? Nothing less than a revolution. The revolutionary? A reactionary, God-believing Protestant, the scholar Gottfried Wilhelm Leibniz (1646-1716)!

What Descartes suspected at the beginning of the 17th century, namely the division of the world into subject and object, finds a kind of culmination in Leibniz at the end of the century. Ironically, it was also the belief of the last polymath that made Leibniz see the world in binary terms. Leibniz developed the so-called "dyadic", a number system in which all numbers were represented only by 0 or 1. Every modern computer is based on this idea, which at first glance seems completely crazy!

Leibniz developed a calculating machine, which he also improved four times. Probably none of the devices worked particularly well because the precision mechanical challenges exceeded contemporary possibilities; a functional replica was not achieved until 1990. But the invention was indicative of the step into modernity that its inventor took: "It is unworthy to waste the time of excellent people with menial arithmetic work ..."

Leibniz's calculating machine. Image and text LeibnizCentral.de: "When the polymath Gottfried Wilhelm Leibniz presented the first model of a calculating machine capable of all four basic arithmetic operations in 1673, it was a milestone in technological development. Over four decades, Leibniz developed the machine."

Leibniz's calculating machine. Image and text LeibnizCentral.de: "When the polymath Gottfried Wilhelm Leibniz presented the first model of a calculating machine capable of all four basic arithmetic operations in 1673, it was a milestone in technological development. Over four decades, Leibniz developed the machine."

Leibniz covered this very modern world view with a binary net of ones and zeros. For him, not only mathematics consisted of 1 and 0, but the whole world could be described in this way. After all, Leibniz also believed, in the sense of the ancient Pythagoreans, that the entire perceptible world could be viewed through mathematical glasses: our language, even the thought processes in our heads, everything is somehow contained in numbers and is based on numbers.

Leibniz, a devout Christian, followed the premise: "Without God there is nothing." This led him to the equation: God is 1, nothingness is 0. This was not a moral valuation of numbers or the world, but a pure description - which may seem anything but modern to us. It finds a parallel in the Far Eastern idea of Yin and Yang, the opposing forces, which however do not fight each other in the sense of good and evil, but complement and mutually condition each other.

Is our binary world the best possible?

Leibniz tried to understand the world and strived for universal harmony. His ideas helped to finally overthrow the previous world view. Since then, our gaze has always been directed toward the future, through two pairs of glasses marked 1 and 0.

And change is the modern aspect of this worldview. When Leibniz made the statement, which is still misunderstood today, that our world is "the best of all possible worlds", he did not call for resting contentedly in his armchair. On the contrary! Leibniz understood our world as changeable, dynamic, full of potential. We can shape what is to be from what is; the best we can only imagine.

The binary number system has led to algorithms - Google, Facebook, even your smart refrigerator works with algorithms. Human relationships no longer have a place as operators, at least in business and technology.

A room full of mathematical formulas.

A room full of mathematical formulas.

This revolution in thinking occurred when modern credit money emerged and the market economy established itself as the dominant economic system. A coincidence?

Probably not. The subject-object split, which Descartes was the first to suspect, finds its consequence in the 1 And 0 of Leibniz. But its origin lies, according to Eske Bockelmann, in the so-called thinking reflex, which developed in the 16th century. And this has a lot to do with our modern money.