Euklid. Gesammelte Werke
Publiziert in lateinischer Sprache von Johann Herwegen, Basel 1537

Vom Stoff mittelalterlicher Klosterschulen zum Basiswissen jedes italienischen Renaissancemalers: Euklid und seine Werke hatten Bestand. Ohne ihn und seine Theorie der Optik wäre die Zentralperspektive eventuell nie entdeckt worden.
Wenn Schüler heute mit kariertem Schulheft, Geodreieck und Zirkel über die Konstruktion geometrischer Formen grübeln, dann stehen sie in einer Tradition, die weit ins Mittelalter zurückreicht: Schon in den Klosterschulen gehörte die Geometrie Euklids zum Lehrplan.
Wie vermittelt man die Grundlagen der Geometrie?
Wir kennen heute den „Lehrplan“, den alle Klosterschüler durchliefen, als die sieben freien Künste: Grammatik, Rhetorik und Dialektik in der Grundstufe, Arithmetik, Geometrie, Musik und Astronomie in der Oberstufe. Dieser Wissenskanon galt bis weit in die frühe Neuzeit als verbindlich. Er war die Grundlage für jeden Studenten, der sich an einer Universität einschreiben wollte.
Das wichtigste Lehrbuch im Fach Geometrie stammte aus der Feder des griechischen Mathematikers Euklid. Seine „Elemente“ beherrschten das Fach bis zum Jahr 1830(!) derart, dass wir die Geometrie bis zur dritten Ebene - also Linie / Quadrat / Würfel - immer noch als euklidische Geometrie bezeichnen.
Dabei wissen wir über den historischen Euklid nicht allzu viel. Er dürfte um das 4./3. Jahrhundert v. Chr. am Museion im ägyptischen Alexandria gewirkt haben. Doch seine Lebensgeschichte ist für unsere Zwecke völlig irrelevant. Es ist sein Buch, die „Elemente“, das im Mittelalter Karriere machte. Es beschäftigt sich ausgehend vom Punkt mit der Konstruktion von Linien und Körpern und fasste damit das geometrische Basiswissen für jeden zusammen, der den Bauplan für eine Kirche entwerfen wollte. Quadrate und Kreise nebeneinander oder übereinander geschichtet waren Jahrhunderte lang die Formen, mit denen Baumeister Gebäude konstruierten. Deshalb standen die Elemente von Euklid in hohen Ehren. In jeder besseren Klosterbibliothek existierte mindestens eine Handschrift.

Die Geometrie unterrichtet Mönche in der Konstruktion von Bauformen. Sie hält in der rechten Hand den Zirkel, in der linken das Dreieckslineal und beschreibt damit Bauformen in eine Staubtafel. Buchillustration vom Beginn des 14. Jahrhunderts. British Library.
Die Geometrie unterrichtet Mönche in der Konstruktion von Bauformen. Sie hält in der rechten Hand den Zirkel, in der linken das Dreieckslineal und beschreibt damit Bauformen in eine Staubtafel. Buchillustration vom Beginn des 14. Jahrhunderts. British Library.
Was die Mathematik mit Gott verbindet
Nun lasen unsere Mönche mit der gleichen Begeisterung Euklid, mit der sie auch die Werke der antiken Kirchenväter rezipierten. Und die beschäftigten sich ebenfalls mit der Mathematik. Denn vieles übernahmen Augustinus & Co. von Platon und Pythagoras - ja, genau, von dem Philosophen, nach dem der bekannte Satz benannt wurde. Deshalb fand sowohl die Formel a2+b2=c2 Eingang in die christliche Erziehung, als auch Platons Behauptung, dass die Geometrie zur „Erkenntnis des ewig Seienden“ führe. Platon sah in perfekten Kreisen und Quadraten das Göttliche, während er die keinen geometrischen Regeln unterliegenden Gegenstände der materiellen Welt für einen matten Abglanz vom Licht der gleißenden Ideen hielt.
Damit inspirierte er prachtvolle Kirchen, die nach streng geometrischen Regeln errichtet wurden. Der Kreis galt als Abbild des Himmels, als Symbol dafür, dass sich dieser um Gottvater drehe, genauso wie der Kreis um den Punkt gezogen wird. Das Quadrat dagegen stand für die Erde mit ihren vier Himmelsrichtungen. Wenn ein Architekt also mit Hilfe der bei Euklid gelernten Methoden die quadratische Vierung einer Kathedrale mit einer über einem Kreis konstruierten Kuppel überwölbte, dann war das die Stein gewordene Botschaft, dass der Gläubige von der irdischen Welt in den Himmel aufzusteigen in der Lage war.

Die Kuppel über dem Quadrat: Stein gewordene Botschaft zur Verbindung zwischen Irdischem und Jenseits. Foto: Dean Strelau, cc-by 2.0
Die Kuppel über dem Quadrat: Stein gewordene Botschaft zur Verbindung zwischen Irdischem und Jenseits. Foto: Dean Strelau, cc-by 2.0

Eine moderne Rekonstruktion des ersten Bildes mit Zentralperspektive, wie es Bruneleschi gemalt haben dürfte. Foto: sailko, cc-by 3.0
Eine moderne Rekonstruktion des ersten Bildes mit Zentralperspektive, wie es Bruneleschi gemalt haben dürfte. Foto: sailko, cc-by 3.0

Filippo Brunelleschi und seine berühmte Kuppel von Florenz Der italienische Architekt und Ingenieur Filippo Brunelleschi war eine der einflussreichsten Persönlichkeiten der italienischen Renaissance und gilt als einer der Gründerväter der Renaissance-Architektur. Wie viele bemerkenswerte Architekten dieser Zeit war Brunelleschi nicht nur Architekt. Er war Ingenieur, Künstler, Bildhauer, Planer, Schlosser, Schiffskonstrukteur, Metallverarbeiter und vieles mehr.
Filippo Brunelleschi und seine berühmte Kuppel von Florenz Der italienische Architekt und Ingenieur Filippo Brunelleschi war eine der einflussreichsten Persönlichkeiten der italienischen Renaissance und gilt als einer der Gründerväter der Renaissance-Architektur. Wie viele bemerkenswerte Architekten dieser Zeit war Brunelleschi nicht nur Architekt. Er war Ingenieur, Künstler, Bildhauer, Planer, Schlosser, Schiffskonstrukteur, Metallverarbeiter und vieles mehr.
Mathematik wird chic
Jahrhundertelang war die Geometrie für die Architekten existentiell und spielte trotzdem im Leben der anderen Menschen eine ähnlich unwichtige Rolle, wie sie es heute noch tut: Man lernt die Konstruktion eines gleichschenkligen Dreiecks in der Schule und vergisst sie dann so bald wie möglich. Welchen Grund gäbe es schon in einem normalen Durchschnittsleben, ein gleichschenkliges Dreieck zu konstruieren?
Doch dann adaptierte das Abendland irgendwann zwischen Spätmittelalter und Frührenaissance die arabischen Zahlen. Sie ermöglichten völlig neue Formen des Rechnens, und damit wurde die Mathematik auf einmal etwas, über das viele Intellektuelle sprachen und schrieben. Es war chic, in der Lage zu sein, schwierige mathematische Probleme zu lösen. Fürsten hielten sich begabte Mathematiker und begannen, sich selbst mit der Mathematik zu beschäftigten. Man unterhielt sich bei Gesellschaften und in Briefwechseln damit, dem Gegenüber ein möglichst kompliziertes mathematisches Problem vorzulegen, und dann demjenigen zu applaudieren, der es aufzulösen verstand. Humanisten und Künstler, die das Interesse eines Mäzens auf sich lenken wollten, taten also gut daran, zumindest die Grundzüge der Mathematik zu beherrschen.
Besonders hart dürfte die Konkurrenz um potente Mäzene zu Beginn des 15. Jahrhunderts in Florenz gewesen sein, wo eine Reihe von hervorragenden Künstlern um gut bezahlte Projekte buhlten. Einer von ihnen war Filippo Brunelleschi (1377-1446). Er verblüffte die Florentiner Kunstwelt im Jahr 1410 mit einer Attraktion: Er schuf ein perspektivisch korrektes Bild vom Baptisterium, indem er sich zum ersten Mal seit der Antike der Linearperspektive bediente. Ein Betrachter soll damals, wie uns Vasari überliefert, nicht in der Lage gewesen sein, einen Unterschied zwischen dem Spiegelbild des Baptisteriums und Brunelleschis gemaltem Bild zu finden.
Und was hat nun Euklid damit zu tun?
Die Inspiration zu seinem innovativen Bild verdankte Brunelleschi Euklids Werk mit dem Titel Optika (= Optik). Darin beschreibt der griechische Mathematiker seine Theorie über das Sehen. Es dreht sich um die Frage, wie ein Auge seine Umgebung wahrnimmt. Für Euklid senden alle Gegenstände Sichtstrahlen aus, die in Form eines Kegels auf das Auge treffen. Er formulierte seine Hypothese als ein geometrisches Problem, indem er die Einfallswinkel der Strahlen aufs Auge berechnete.
Sein Sichtkegel ist nach streng geometrischen Grundsätzen aufgebaut: Was näher ist, scheint uns wegen des engeren Sichtkegels größer, was weiter entfernt ist, wirkt kleiner. Euklid lieferte Brunelleschi mit seiner Schrift Optika die theoretischen Grundlagen dafür, auf Grund mathematischer Gesetze zu konstruieren, wie er das Baptisterium zeichnen müsse, um es trotz des flachen Untergrundes dreidimensional wirken zu lassen.
Euklids Optik, die Erfindung der Perspektive und ihre Anwendung
Das erste uns erhaltene Gemälde, das gemäß Euklids Linearperspektive konzipiert wurde, ist ein Fresko des Florentiner Künstlers Masaccio. Die Kassetten des Tonnengewölbes verkleinern sich systematisch entlang der Fluchtlinien von vorne nach hinten. Das Bild bringt die Perspektive ins Spiel. Generationen von Künstlern sollten sich an der Beherrschung der Perspektive abarbeiten und sie zu immer neuen Höhenflügen führen. Glanzpunkt dieser Entwicklung sind die Freskos des Rokoko. Meistern ihrer Kunst gelang es, mittels der virtuos angewandten Gesetze der Perspektive auf einer praktisch flachen Kirchendecke einen Blick in den nach oben offenen Himmel darzustellen.
Die Grundlage für all das, war Euklid. Durch ihn wurden Geometrie und Malerei zu zwei Seiten einer Münze. Nach Massacio kam kein Künstler, der für modern gelten wollte, um ausgedehnte mathematische Studien herum. Und das hatte für ihren Stand einen angenehmen Nebeneffekt: Vorbei waren die Zeiten, als die Malerei als reines Handwerk galt. Nun stand die Theorie im Mittelpunkt, und das mit allen sozialen Folgen. Der Künstler kletterte die gesellschaftliche Leiter nach oben. Es öffnete sich ihm der Zugang zum Fürstenhof. Er diskutierte als Gleichrangiger mit Humanisten, Politikern und Höflingen. Wobei gerade die Höflinge alles andere als erfreut waren über die neue Konkurrenz.
Wie schwer sie den Eindringlingen das Leben machten, illustriert eine Anekdote aus dem Leben von Leonardo da Vinci: Er war zu Gast am Hof des Ludovico Sforza und forderte geradezu von ihm die Gelegenheit, im gelehrten Rededuell – ja, so etwas gab es damals, und es war richtig beliebt - seine Bildung zu zeigen. Im Februar des Jahres 1498 kamen alle Mitglieder des Hofes von Ludovico Sforza zusammen, um zu sehen, wie sich dieser uneheliche Sohn eines kleinen Advokaten aus Vinci gegen die hochlöblichen Adligen und studierten Doktoren der Universitäten schlagen würde. Natürlich ging Leonardo als Sieger aus diesem Rededuell hervor, auch weil er einen guten Mathematiklehrer gehabt hatte.
Sein Freund Luca Pacioli gehört nämlich zu den größten Mathematikern seiner Zeit. Von ihm lernte Leonardo da Vinci die Gesetze der Perspektive, die er in seinem späteren Leben so meisterhaft anwenden sollte. Die beiden Genies tauschten sich sowohl über Fragen der Kunst als auch über mathematische Probleme miteinander aus, und die gemeinsame Frucht ihrer Überlegungen floss in das 1509 veröffentlichte Buch „De divina proportione“ (= Über die göttlichen Verhältnisse) ein. Leonardo da Vinci illustrierte höchstpersönlich den von Luca Pacioli verfassten Text über den Goldenen Schnitt.
Dass die „Elemente“ des Euklid mit ihrer Grundlagenforschung zur Geometrie für Pacioli „elementar“ war, bringt ein 1495 entstandenes Porträt auf den Punkt: Die Hand des genialen Mathematikers ruht beim Entwerfen einer geometrischen Figur auf den Schriften Euklids.
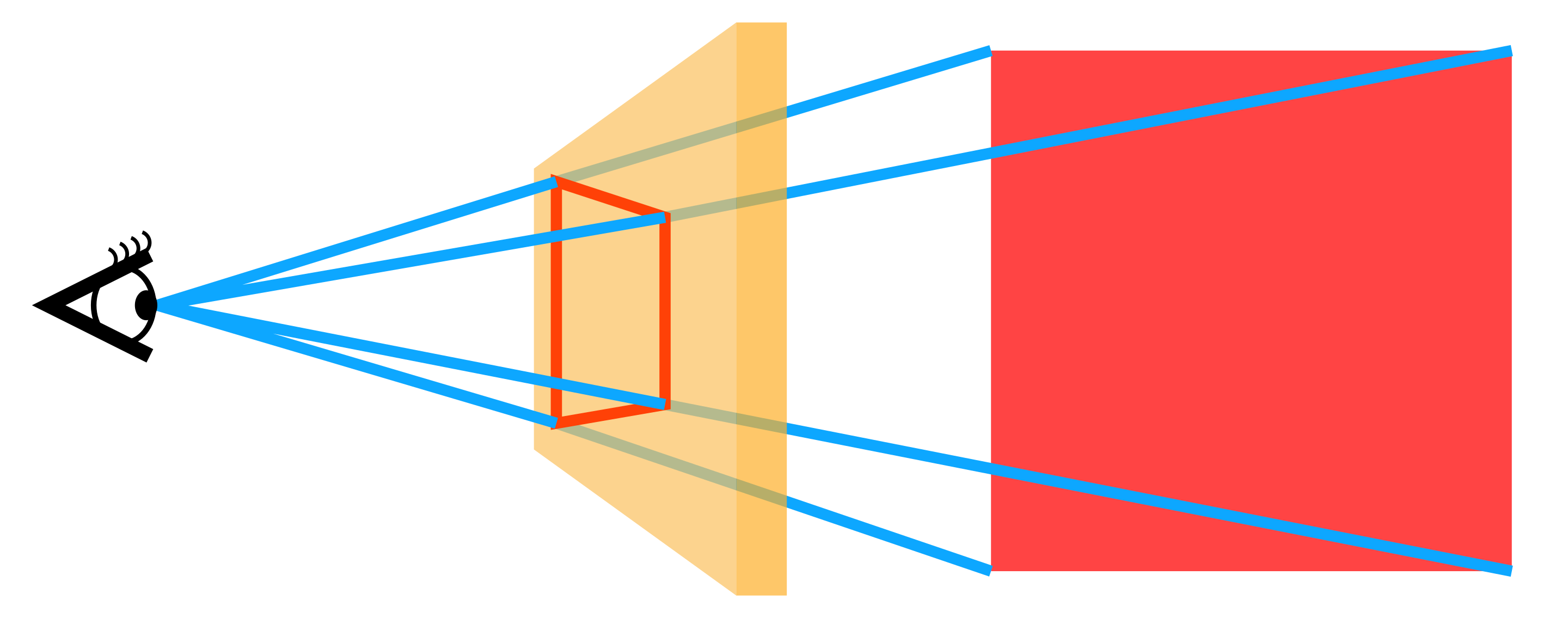
Graphische Darstellung der Theorie der Optik von Euklid. Graphik: Marco Polo / Wikipedia.
Graphische Darstellung der Theorie der Optik von Euklid. Graphik: Marco Polo / Wikipedia.

Masaccio schuf dieses Fresko zwischen 1425 und 1428. Es ist das erste erhaltene Werk der europäischen Kunstgeschichte, das die Linearperspektive systematisch anwendet.
Masaccio schuf dieses Fresko zwischen 1425 und 1428. Es ist das erste erhaltene Werk der europäischen Kunstgeschichte, das die Linearperspektive systematisch anwendet.

Ein Höhepunkt der auf Euklid basierenden, perspektivischen Kunst: St. Maria-de-Victoria in Ingolstadt. Die Decke, auf der dieses Gemälde zu finden ist, ist praktisch flach. Foto: KW
Ein Höhepunkt der auf Euklid basierenden, perspektivischen Kunst: St. Maria-de-Victoria in Ingolstadt. Die Decke, auf der dieses Gemälde zu finden ist, ist praktisch flach. Foto: KW

Porträt des Luca Pacioli aus dem Jahr 1495: Seine Hand ruht auf dem Werk Euklids, während rechts davon sein eigenes Buch, die gerade eben gedruckte Summa zu sehen ist. Pacioli konstruiert eine geometrische Figur aus des Lehrbuch Euklids: ein in einem Kreis eingeschriebenes Dreieck.
Porträt des Luca Pacioli aus dem Jahr 1495: Seine Hand ruht auf dem Werk Euklids, während rechts davon sein eigenes Buch, die gerade eben gedruckte Summa zu sehen ist. Pacioli konstruiert eine geometrische Figur aus des Lehrbuch Euklids: ein in einem Kreis eingeschriebenes Dreieck.
Der Basler Euklid
Bald sprachen nicht mehr nur die italienischen Künstler über die Bedeutung von Euklid. Seine Werke wurden auch jenseits der Alpen zur Pflichtlektüre. Albrecht Dürer war ein wichtiges Glied in der Kette des Wissenstransfers. Ihm ist ein weiterer Teil unseres Essays „Mathematik: Königin der Wissenschaft“ gewidmet sein.
Der Basler Verleger Johann Herwegen witterte ein hervorragendes Geschäft und publizierte 1537 eine Gesamtausgabe der Werke des griechischen Mathematikers. Sie enthält weit mehr als die seit dem Mittelalter bekannten Elemente. Der Käufer erhielt zusätzlich die für Künstler so wichtige Optik und einige weitere kleinere Schriften des großen Mathematikers.


Wieso schreibt ein Reformator ein Vorwort zu Euklid?
Die im MoneyMuseum aufbewahrte Ausgabe des Euklid von 1537 ist etwas ganz Besonderes, denn der bekannte protestantische Theologe und Weggefährte Martin Luthers schrieb ein Vorwort dazu. Das sollte uns nicht verwundern: Das Interesse von humanistischen Wissenschaftlern und Theologen an der Mathematik war enorm. Sie fühlten sich vor allem von der jüdischen Kabbalistik inspiriert. Ziel der Kabbala ist es, die Buchstaben der Bibel in Zahlenwerte umzusetzen, um durch komplizierte mathematische Berechnungen Einsicht in Gottes Plan zu erhalten. Das leuchtete – zumindest damals – auch protestantischen Theologen ein, die davon ausgingen, dass das Ende der Welt nahe sei.

Die Widmung Melanchthons im Basler Euklid von 1537
Die Widmung Melanchthons im Basler Euklid von 1537

Das Porträt von Philipp Melanchthon, gemalt 1543 von Lukas Cranach.
Das Porträt von Philipp Melanchthon, gemalt 1543 von Lukas Cranach.
